Advent of Code 2025
Advent of Code is “an Advent calendar of small programming puzzles.” I had a great experience participating in it last year, so I did it again this year. For whatever reason, I found the puzzles this year a lot easier–maybe the creator went easy on us, or maybe I just got better at programming. I thought the most interesting ones were the puzzles on day 9 and day 10.
Day 09
Edit: also checkout my writeup on day 10!
To summarize, for day 9 (part 2), you’re given a big list of coordinates. These coordinates form a boundary, and you’re asked to find the largest “valid” rectangle parallel to the X and Y axes that is fully contained within the boundary, where a “valid” rectangle is one which has two of its opposite corners are from the coordinate list and its sides are parallel to the XY axes. (For the more detailed version, see: https://adventofcode.com/2025/day/9
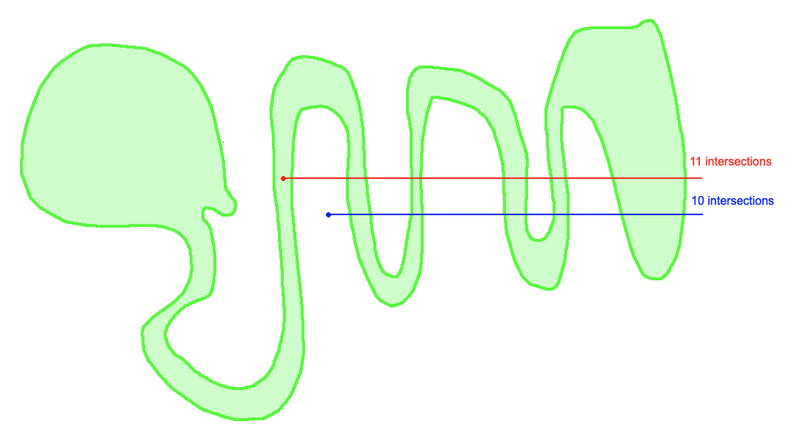
This problem took me a while to solve because I got stuck on a few things.
First, I spent a lot of time looking for a solution
that was better than O(n^3) time before eventually realizing
that it probably doesn’t exist (where n is the number of
coordinates). There are n^2 different valid rectangles to
check, so for the solution to be better than O(n^3), you’d
need to either check every rectangle in less than O(n) time,
or you’d need to not check every rectangle. I tried doing some
stuff with heaps, but eventually became convinced that it wasn’t
possible.
After deciding that better than O(n^3) was impossible, I started
to look for ways to verify a rectangle in O(n). The
most intuitive and obvious way to do this is to check every
side of the rectangle to see if it overlaps with any of the
edges in the boundary. This would be O(n) time because
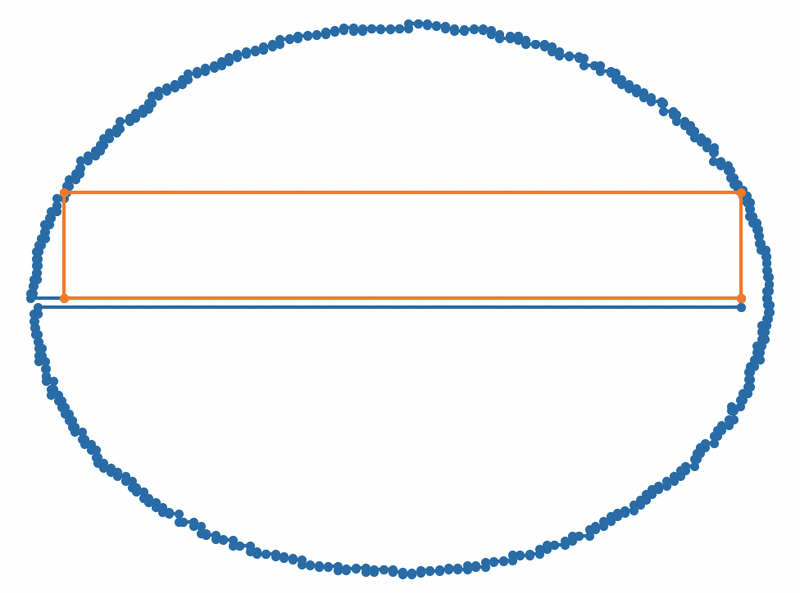
there are 4 sides and n boundary edges. However, there is
an edge case to consider: sometimes, a side of a rectangle may
line up exactly with an edge without going outside of the
boundary. For example, see the diagram below:


How to deal with this edge case? I made it so that the rectangle
“never” aligns exactly with a boundary–it either crosses it or
it doesn’t. I did this by abusing the fact that every coordinate
was an integer… so I just “nudged” the rectangle inwards by
0.01. This way, the rectangle sides were never integer, and
the boundary edges were always integers, so I don’t need to deal
with the edge case.
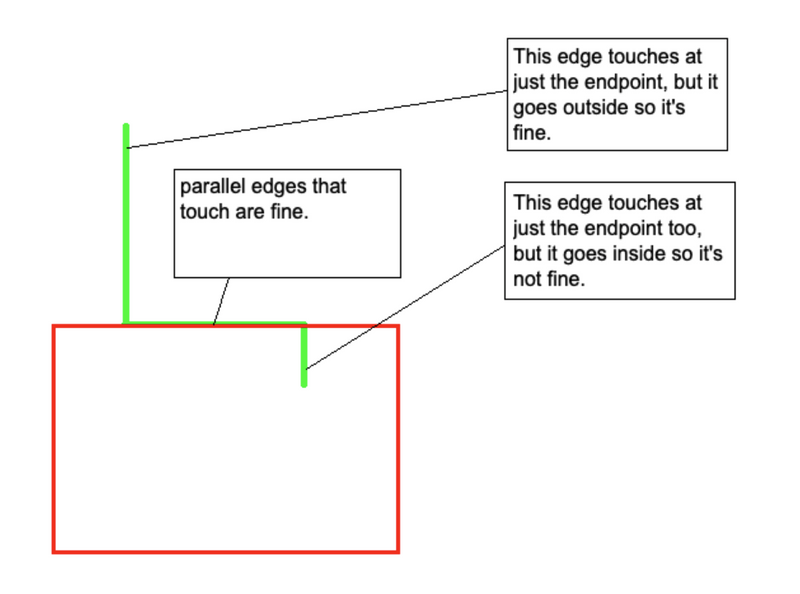
For the general (non-integer) case, you can just notice that the real trouble comes from when the rectangle intersects a boundary edge at only an endpoint. In these cases, the edge either goes inside or goes outside of the rectangle. I figured this out from discussing our solutions with a friend the next day.
This approach (check every rectangle against every edge with nudging) worked, and my program was able to find the optimal rectangle.
Bonus
This didn’t end up working, but a neat thing I learned while working on this problem is there is a really easy way to check if a point is inside or outside some boundary: simply draw a ray from that point in any direction and count the number of times it intersects the boundary. If it intersects an odd number of times, then it is inside. Even, then it is outside.
This doesn’t work for the problem because to do the same thing for a rectangle, you would have to do the check for every point on the rectangle. Normally, this would be infinite, but since we’re working with integers, it just ends up being a very large number of points to check.